1/58ページ
ダウンロード(11.2Mb)
ドライブシステムの選定に必要な様々な数式をご紹介
ドライブシステムの構築をフロー別にわかりやすく、必要な数式と共にご紹介します。
このカタログについて
| ドキュメント名 | 数式集 |
|---|---|
| ドキュメント種別 | ハンドブック |
| ファイルサイズ | 11.2Mb |
| 取り扱い企業 | マクソンジャパン株式会社 (この企業の取り扱いカタログ一覧) |
この企業の関連カタログ

このカタログの内容
Page1
数式集
Formulae Handbook
Jan Braun
VCC ≥ nL ML
maxon academy
Page4
序文
本数式集には、ドライブシステムに必要なすべてのコンポーネントと関連して最も重要
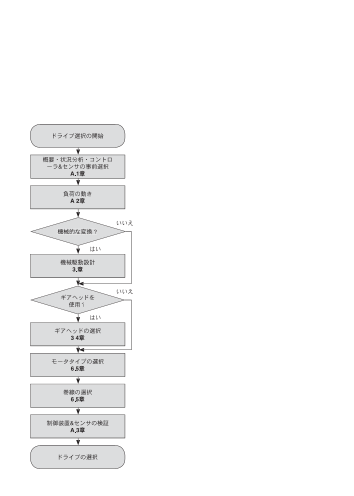
な計算式がリストアップされています。フローチャートを使用することで、駆動を素早
く選択できるようになっています。多くの図解、記号についての明確な説明が、数式の
理解に役立ちます。
本書にはマクソン総合カタログ、さらにmaxon academy 出版の書籍『The selection of
high-precision microdrives 』からの最も重要な数式が集められています。
本数式集を編集する動機は、マクソンDCドライブ(約500W以下の小型・高出力ド
ライブユニット)の50年にもおよぶサクセスストーリーを綴った『The selection of
high-precision microdrives 』(Dr. Urs Kafader 著)です。この数式集は上記の書を補
完する目的で、エンジニア・講師・学生を対象に執筆されました。
謝辞
まずは本数式集を執筆する勇気を与えてくださったDr. Urs Kafaderに感謝の意を表明し
ます。完璧なレイアウトとイラストはパトリシア・ガブリエル氏とベニ・アンデルハル
デン氏によるものです。ウアス・カファデル氏、バルバラ・シュルプ氏、アニヤ・グノ
ス氏、シュテファン・バウマン氏、マルティン・リュエッグ氏、ミヒャエル・バウムガ
ルトネル氏、マルティン・ヴィンドリン氏、イエンツ・シュルツェ氏、アルベルト・ブ
ヘリ氏、マルティン・オーデルマット氏、そしてヴァルター・シュミット氏には、原稿
に目を通していただき、貴重なアドバイスをいただきました。maxon motor ag の大勢
のスタッフには、私の疑問に対して惜しみないサポートをいただきました。
ザクセルン市、2016 年 春
Jan Braun
第3版 2016年
© 2016, maxon academy
本著作は著作権により保護されます。特に外国語への翻訳、複製、データ処理システム
への保存、転載、口頭発表における、すべての権利を留保します。この著作内で商標登
録マークや一般名称などが言及されることは、これらが商標法において保護されていな
いということにはなりません。この著作にあるすべての情報(特に数値データ、アプリ
ケーション、量的データ、ならびに助言や提言)は、慎重に調査されたものですが、誤
字脱字のような精度を保証することはできません。ここに提供する情報の正確さは、個
々の事例においてユーザ自身が確認する必要があります。著者、出版社および/または
その代理人は、人身傷害、物的損害、金銭的損失に対して責任を負いません。
Page13
立体図形 図 質量、慣性モーメント
m = 43 · ρ · π · (r 3
a − r 3
i )
中空球
2 r 5 − r 5
Jx = Jy = Jz = 5 · m · a i
r 3
a − r 3
i
m = ρ · a · b · c
直方体
J 1
x =
2
12 · m· (b + c2)
m = ρ · A · l
細い棒 y
J = J 1
1
x z = 2 · m · l2
m = 13 · ρ · a · b · h
四角錐 J 1
x = 2 0 · m · (a2 + b2)
Jy = 1 · m · (b2 + 320 4 h
2)
x2
m = ρ · π · ∫
x1 f 2(x) · dx
任意の回転体 1 x2
Jx = 2 · ρ · π · ∫
x1 f 4(x) · dx
シュタイナーの定理
重心Sを通る軸 sに、rs の距離 Jx = m · r 2
s + Js で、ある平行な回転軸xに関
する慣性モーメント
記号 名称 SI 単位 記号 名称 SI 単位
A 断面積 m2 h 高さ m
Js 重心Sの中心を通る軸sに関する l 長さ m
慣性モーメント kgm2 m 質量 kg
Jx 回転軸xに関する慣性モーメント kgm2 ra 外半径 m
Jy 回転軸yに関する慣性モーメント kgm2 ri 内半径 m
Jz 回転軸zに関する慣性モーメント kgm2 rs 軸sの重心Sからの距離 m
a a辺の長さ m ρ 密度 kg/m3
b 辺bの長さ m x1 x軸上の点 1 m
c 辺cの長さ m x2 x軸上の点 2 m
maxon Formulae Handbook 13
Page17
3/3 台形 三角形
最小加速度/力のために最適化(ΔsとΔt
最小出力のために最適化(ΔsとΔtが与え が与えられている時)
られている時):熱的に最も有利 最小時間要件のために最適化(Δsとamaxが
与えられている時)
v
v max
max
∆s ∆s
∆ttot ∆ttot
vmax = 1.5 · Δs
Δt v = 2 · Δs
max
tot Δttot
a · Δs
max = 4.5 Δt 2 amax = 4 · Δs
tot Δt 2
tot
Δttot = 1.5 · Δs
v Δt 2 · Δs
max tot = vmax
v 2 v 2
amax = 2 · max ax
Δs a m
max = Δs
Δt 3 Δs ≈ 2.12 · Δs s
tot = 2 · a Δttot = 2 · Δ
a
max amax max
v 1
max = · Δs · amax ≈ 0.7 · Δs · amax vmax = Δs · a
2 max
Δs = 2 1
3 · Δttot · vmax Δs = 2 · Δttot · vmax
v v
amax = 3 · max
Δt amax = 2 · max
tot Δttot
Δs = 2
9 · a 2
max · Δttot ≈ 0.22 · a 2
max Δttot Δs = 14 · amax · Δt 2
tot
v x =
1
3 · a Δt v = 1 · a
ma max · Δttot ≈ 0.33 · amax tot max 2 max · Δttot
v 2 v 2
Δs = 2 · max
a Δs = max
max amax
v v
Δttot = 3 · max
a Δt 2 · max
max tot = amax
記号 名称 SI 単位 記号 名称 SI 単位
amax 最大加速度 m/s2 Δs 距離 m
vmax 最大速度 m/s Δttot 総時間 s
maxon Formulae Handbook 17
Page18
2.4 典型的な回転運動プロファイル
プロファイル 一般情報 対称
限られた回転数での長い回
適合性
転運動
n n
max max
∆φ ∆φ
ダイヤグラム
∆ta ∆tb ∆tc ∆ta ∆tb ∆ta
∆ttot ∆ttot
タスク:
n = 3 0 · Δφ 30
max π Δt Δtc nmax = · Δφ
tot −
Δta + π (Δttot − Δta)
角 Δφ Δt 2
を時間内 tot に進む Δφ
α Δφ
max = α
Δt − Δta + Δtc max = (Δt
tot 2 ·Δta tot − Δta) · Δta
Δt = 30 Δφ Δta + Δt
· c 30 Δφ
Δt
角 Δφ を tot = π · + Δt
制限された回転数 tot π n +
max 2 nmax a
n n π n
max で進む π
α a α
max = 0 · m x
3 Δt max =
max
30 · Δt
a a
Δφ
Δt
角 Δφ を制限された角加速 tot = α Δta
max · Δt +
a
度 αmax で進む
n 30
max = π · αmax · Δta
π Δt + Δt π
Δφ = a c
動きを時間内 Δt 30 · n m a x · (Δttot − Δta)
tot に最小回 30 · n Δφ =
max · 2 + Δtb
転数 n π n π n
max で完了する α ax α max
max = 3 0 ·
m
Δt max =
a 3 0 · Δta
Δφ = α
動きを時間内 Δt max · (Δttot − Δta) · Δta
tot に最大角
加速度 αmax で完了する nmax =
30
π · αmax · Δta
制限された回転数 nmax と
制限された角加速度 αmax
の動き
記号 名称 SI 単位 記号 名称 SI 単位
αmax 最大角加速度 rad/s2 Δφ 回転角度 rad
Δta 時間 a s
Δtb 時間 b s 記号 名称 maxon
Δtc 時間 c s nmax 負荷サイクルの最大回転数 rpm
Δttot 総時間 s
18 maxon Formulae Handbook