1/12ページ
ダウンロード(2.8Mb)
「シャノンの第一定理」情報とエントロピーの関係(情報が増えるとエントロピーは減少する)
「シャノンの第一定理に関する経験」ーーオリジナル技術開発ーー
1) テーマ
「シャノンの第一定理が、具体的に経験上で役に立つ」
1-1)基本システムの考察(注1)に関する
モデル作成として役に立つ
1-2)データとノイズに関する基礎事項として役に立つ
(ルーチンワーク的な開発業務の中では
必要性を理解しにくいが、
オリジナリティの高い、新製品の研究開発の
立場で考えると、
研究の視点(注2)としてとして大変有効
注1:例 システム開発に関するオブジェクト
(アルゴリズム 等)の整合性・体系化
注2:例 機械振動・電気ノイズ・プログラム
バグ・不具合・・の原因解析
・・・・
関連メディア
このカタログについて
| ドキュメント名 | 「シャノンの第一定理に関する経験」ーーオリジナル技術開発ーー |
|---|---|
| ドキュメント種別 | 事例紹介 |
| ファイルサイズ | 2.8Mb |
| 取り扱い企業 | 超音波システム研究所 (この企業の取り扱いカタログ一覧) |
この企業の関連カタログ

このカタログの内容
Page1
シャノンの第一定理に関する経験
1) テーマ
「シャノンの第一定理が、具体的に経験上で役に立つ」
1-1)基本システムの考察(注1)に関する
モデル作成として役に立つ
1-2)データとノイズに関する基礎事項として役に立つ
(ルーチンワーク的な開発業務の中では
必要性を理解しにくいが、
オリジナリティの高い、新製品の研究開発の
立場で考えると、研究の視点(注2)としてとして大変有効
注1:例 システム開発に関するオブジェクト
(アルゴリズム 等)の整合性・体系化
注2:例 機械振動・電気ノイズ・プログラム
バグ・不具合・・の原因解析
Page2
2) 基礎知識
理論と歴史の流れ
* サイバネティクス(フィードバック)から
情報の単位としてビットが基準になるまで
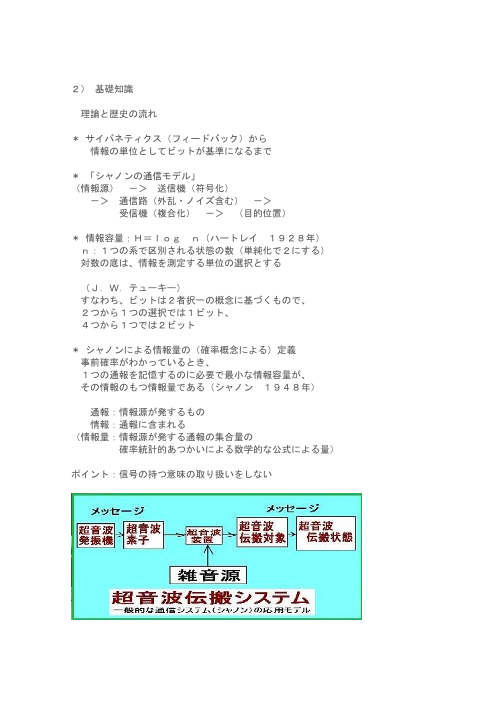
* 「シャノンの通信モデル」
(情報源) -> 送信機(符号化)
-> 通信路(外乱・ノイズ含む) ->
受信機(複合化) -> (目的位置)
* 情報容量:H=log n(ハートレイ 1928年)
n:1つの系で区別される状態の数(単純化で2にする)
対数の底は、情報を測定する単位の選択とする
(J.W.テューキー)
すなわち、ビットは2者択一の概念に基づくもので、
2つから1つの選択では1ビット、
4つから1つでは2ビット
* シャノンによる情報量の(確率概念による)定義
事前確率がわかっているとき、
1つの通報を記憶するのに必要で最小な情報容量が、
その情報のもつ情報量である(シャノン 1948年)
通報:情報源が発するもの
情報:通報に含まれる
(情報量:情報源が発する通報の集合量の
確率統計的あつかいによる数学的な公式による量)
ポイント:信号の持つ意味の取り扱いをしない
Page3
3) 基礎知識の理解
「基礎知識を深めると重要な定理や法則が理解できる」
* 「シャノンの第一定理」
情報とテントロピーの関係
(情報が増えるとエントロピーは減少する)
エントロピー:無記憶情報源のシンボル当たりの平均情報量
(情報量*確率の総和)
無記憶情報源<->マルコフ情報源
(その情報以前の有限個(m)の情報に影響される
情報源:m重マルコフ情報源)
情報と確率過程の関係->エルゴード的->
確立の再定義->統計処理->・・
Page4
4) 理解から応用(創造)
経験と実例
4-1)論理は用意されていない ?である
:データとノイズの関係
4-2)考えなければならない:どこから?
何を考えるか?
経路とノイズとデータの特定
(例 ロボットの動作、デジタル解析のデータ
:デジタルアナライザー、
プログラム言語のコンパイラー、システムの取り扱い方法)
ロボットの動作データ(注1 機械・電気・ソフト)と
動作測定によるデータの検討に関する
通信モデルの利用(通信モデルに対する第一定理の保証)
注1:機械(特性) 伸び・たわみ・疲労・・・
電気(信号) 電気的な性質・応答特性・・・
ソフト 制御のアルゴリズム・データ構造・チューニング処理・・・
Page5
4-3)論理モデルをつくる:現象との違いを考察する
解析事例(振動解析 プログラムのバグ解析 人間と言う要因の検討)
振動と言う現象(全体)と測定(ポイント)による
データの論理的考察
時間的変化に対する、
条件の設定と統計やシュミレーション等の解析方法の考察
4-4)論理モデルの限界と現象を考察する
4-5)その現象に対するオリジナルな論理を作成する
新規開発事例(材質、特性、一般理論の組み合わせと現象 :総合力)
理論やデータでは突破できない(注:基礎知識の理解は必要である)
感触やイメージが必要である
Page6
5) 設計思想への発展
オリジナルな理論を忠実に開発・設計し、
一つの製品(システム)にまとめあげることは、
その理論(人)による思想(identity)にまで広がります
そして思想からモデル(システム)の修正や変更が行われ、
繰り返す中で発展していくように思います
このような観点でモノを見ると、良い製品、良い設計にふれることの大切
さが理解できると思います
私は、これが設計する力だと思います
Page7
6) まとめ
* 応用できれば知識は技術力として役に立つ
* 機械・システムの知識も応用できるところまで高めなければいけない
* そのためには、クリアすべき基礎知識がある
結局、好きな部分は基礎知識がわかるまで学習する必要がある
(あるいは、実際に製造工程に取り入れ、理解不足の部分が問題になり
苦労して身につけることになる)
最終的には、設計思想・論理モデルを形成し、深めることが本質だと思います
(そのために観察することと工夫することの重要性をまとめにします
数式や統計処理は有効ですが、各処理のそれぞれの段階も
技術的説明(検討・考察)を行う必要があることの重要性を指摘します)
シャノンのジャグリング定理を応用した「超音波制御」方法
http://ultrasonic-labo.com/?p=1753
統計的な考え方を利用した超音波
http://ultrasonic-labo.com/?p=12202
Page8
<<< 超音波のダイナミック制御 >>>
<超音波のダイナミック制御技術>
http://ultrasonic-labo.com/?p=2301
超音波のダイナミック制御技術を開発
http://ultrasonic-labo.com/?p=2015
オリジナル技術(液循環)
http://ultrasonic-labo.com/?p=7658
<超音波のダイナミックシステム:液循環制御技術>
http://ultrasonic-labo.com/?p=7425
Page9
<<< 超音波の音圧測定・解析 >>>
超音波の相互作用を評価する技術
http://ultrasonic-labo.com/?p=12202
超音波の音圧測定・データ解析技術
http://ultrasonic-labo.com/?p=3829
超音波の音圧測定解析
http://ultrasonic-labo.com/?p=17849
超音波洗浄機の<音圧計測・実験・解析・評価>(出張対応)
http://ultrasonic-labo.com/?p=1934
超音波プローブの製造・評価技術
http://ultrasonic-labo.com/?p=15285
音響流(超音波)制御技術
http://ultrasonic-labo.com/?p=1258
超音波の伝搬現象について
http://ultrasonic-labo.com/?p=2604
Page10
超音波プローブの製造・評価技術
http://ultrasonic-labo.com/?p=15285
非線形振動現象のコントロール技術
http://ultrasonic-labo.com/?p=17418
超音波の音圧測定解析データを公開
http://ultrasonic-labo.com/?p=2387
超音波発振制御システム 2023(25MHz 2ch 200MSa/s)
http://ultrasonic-labo.com/?p=1972
【本件に関するお問合せ先】超音波システム研究所
メールアドレス info@ultrasonic-labo.com
ホームページ http://ultrasonic-labo.com/ 以上
Page12
クロード・シャノン 情報時代を発明した男 (単行本) 単行本 – 2019/6/28
ジミー・ソニ (著), ロブ・グッドマン (著), 小坂 恵理 (翻訳)
携帯電話、電子メール、インターネット、ストリーミング。今日の世界はこの男なし
にはありえなかった。「情報理論の父」と呼ばれる孤高の天才数学者、初の評伝。
出版社 : 筑摩書房 (2019/6/28)
発売日 : 2019/6/28
言語 : 日本語
単行本 : 432 ページ
目次
1 内気な天才数学者
(発明家の遺伝子;工学か数学か;部屋いっぱいの特大の頭脳 ほか)
2 天才の孤独
(大西洋横断通信への挑戦;インテリジェンスから情報へ;爆弾級の発見 ほか)
3 遊ぶ天才
(シャノン教授;内部情報;からくり好きの天国 ほか)
京都賞 第 1 回(1985)受賞
基礎科学部門 数理科学(純粋数学を含む)
クロード・エルウッド・シャノン
https://www.kyotoprize.org/laureates/claude_elwood_shannon/