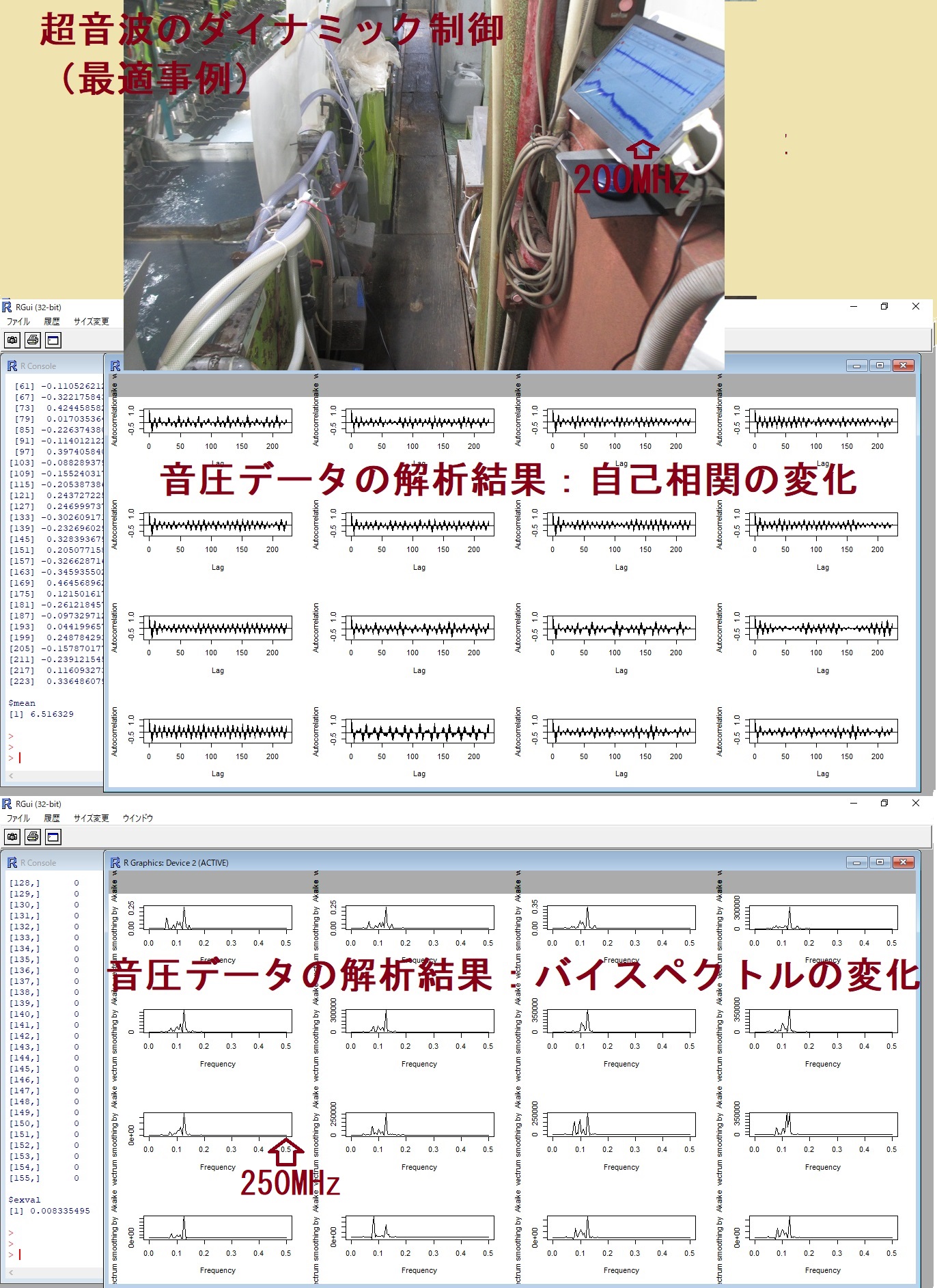
1/25ページ
ダウンロード(4.7Mb)
超音波伝搬状態の解析・評価
<<超音波の音圧データ解析・評価>>
1)時系列データに関して、
多変量自己回帰モデルによるフィードバック解析により
測定データの統計的な性質(超音波の安定性・変化)について
解析評価します
2)超音波発振による、発振部が発振による影響を
インパルス応答特性・自己相関の解析により
対象物の表面状態・・に関して
超音波振動現象の応答特性として解析評価します
3)発振と対象物(洗浄物、洗浄液、水槽・・)の相互作用を
パワー寄与率の解析により評価します
4)超音波の利用(洗浄・加工・攪拌・・)に関して
超音波効果の主要因である対象物(表面弾性波の伝搬)
あるいは対象液に伝搬する超音波の
非線形(バイスペクトル解析結果)現象により
超音波のダイナミック特性を解析評価します
この解析方法は、
複雑な超音波振動のダイナミック特性を
時系列データの解析手法により、
超音波の測定データに適応させる
これまでの経験と実績に基づいて実現しています。
注:解析には下記ツールを利用します
注:OML(Open Market License)
注:TIMSAC(TIMe Series Analysis and Control program)
注:「R」フリーな統計処理言語かつ環境
超音波の伝搬特性
1)振動モードの検出(自己相関の変化)
2)非線形現象の検出(バイスペクトルの変化)
3)応答特性の検出(インパルス応答の解析)
4)相互作用の検出(パワー寄与率の解析)
注:「R」フリーな統計処理言語かつ環境
autcor:自己相関の解析関数
bispec:バイスペクトルの解析関数
mulmar:インパルス応答の解析関数
mulnos:パワー寄与率の解析関数
関連メディア
このカタログについて
| ドキュメント名 | 超音波の音圧データ解析技術(R言語) |
|---|---|
| ドキュメント種別 | 事例紹介 |
| ファイルサイズ | 4.7Mb |
| 登録カテゴリ | |
| 取り扱い企業 | 超音波システム研究所 (この企業の取り扱いカタログ一覧) |
この企業の関連カタログ

このカタログの内容
Page1
超音波の音圧データ解析技術(R言語)
超音波伝搬状態の解析・評価
音圧グラフ 横軸:時間 縦軸:音圧
音圧データの解析(自己相関)
超音波システム研究所
Page2
音圧測定
Page3
1. 準備
解析用データの確認
超音波の音圧測定データ
(例 オシロスコープの測定データ形式 PSDATA ファイル)から
解析用の
Microsoft Office Excel CSV ファイル
を作成・保存してください
例
Page4
2. 解析ソフトの立ち上げ
ダブルクリックして立ち上げる
>| 左記のようなプロンプト表示が行われます
エラー表示が行われた場合には、
その他の作業ファイル・・・を終了してから
もう一度立ち上げてください
Page5
3. 解析ソフトの読み込み
3-1:パッケージ->
ローカルにあるzipファイルからの・・・・
3-2:デスクトップのzipファイル
TIMSAC1.2.1 を選択する
Package‘timsac’ (TimeSeriesAnalysisandControlPackage)
Functionsforstatisticalanalysis,predictionandcontroloftimeseriesbasedmainl
yonAkaikeandNakagawa(1988)
Page6
3-3:読み込み画面の確認
3-4:パッケージの読み込み
パッケージ->パッケージ読み込み・・・ 選択する
Page7
3-5:timsacの選択
3-6:「OK」選択により読み込み
以上で解析準備完了です
Page8
参考
バイスペクトル
バイスペクトルは以下のように
周波数 f1、f 2、f1 + f 2のスペクトルの積で表すことができる。
B( f1 , f 2 ) = X ( f1 )Y( f 2 )Z ( f1 + f 2 )
主要周波数が f1であるとき、
f1 + f1 = f 2、f1 + f 2 = f3で表される f 2、f3という周波数成分
が存在すればバイスペクトルは値をもつ。
これは主要周波数 f1の整数倍の周波数成分を持つこと
と同等であるので、バイスペクトルを評価することにより、
高調波の存在を評価できる。
詳しい説明は専門書・・・を読んで確認してください
エクセルファイルのデータ列
Page9
解析コマンド
dev.off()
par(mfrow=c(2,2)) : 2行 2 列のグラフ表示設定
data11 <- read.table("C:/20191220/20191220-0030/20191220-0030_12.csv",
skip=6, sep=",", nrows=6000)
plot(data11$V2)
data11 <- read.table("C:/20191220/20191220-0030/20191220-0030_12.csv",
skip=6, sep=",", nrows=6000)
spectrum(data11$V2,method="ar")
data11 <- read.table("C:/20191220/20191220-0030/20191220-0030_12.csv",
skip=6, sep=",", nrows=6000)
bispec(data11$V2)
data11 <- read.table("C:/20191220/20191220-0030/20191220-0030_12.csv",
skip=6, sep=",", nrows=6000)
autcor(data11$V2)
Page10
dev.off()
解説 終了
plot(data11$V2)
解説 data11 の 2 番目のデータ列(1chの測定データ)に対して
プロット(音圧測定データのグラフ作成)を行う
spectrum(data11$V2,method="ar")
解説 data11の 2 番目のデータ列(1chの測定データ)に対して
AR(自己回帰)モデルによるスペクトル解析を行う
bispec(data11$V2)
解説 data11の 2 番目のデータ列(1chの測定データ)に対して
バイスペクトル解析を行う
autcor(data11$V2)
解説 data11の 2 番目のデータ列(1chの測定データ)に対して
自己相関の解析を行う
dev.off()
Page11
参考
1)以下のようにテキストデータをコピーしてRの画面にペーストすると
1chと2chのデータ比較ができます
dev.off()
par(mfrow=c(4,2))
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_12.csv", skip=6,
sep=",", nrows=6000)
plot(data11$V2)
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_12.csv", skip=6,
sep=",", nrows=6000)
spectrum(data11$V2,method="ar")
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_12.csv", skip=6,
sep=",", nrows=6000)
bispec(data11$V2)
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_12.csv", skip=6,
sep=",", nrows=6000)
autcor(data11$V2)
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_12.csv", skip=6,
sep=",", nrows=6000)
plot(data11$V3)
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_12.csv", skip=6,
sep=",", nrows=6000)
spectrum(data11$V3,method="ar")
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_12.csv", skip=6,
sep=",", nrows=6000)
bispec(data11$V3)
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_12.csv", skip=6,
sep=",", nrows=6000)
autcor(data11$V3)
Page12
2)以下のようにテキストデータをコピーしてRの画面にペーストすると
すべての解析を連続的に行います
dev.off()
par(mfrow=c(2,2))
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_12.csv", skip=6,
sep=",", nrows=6000)
plot(data11$V2)
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_12.csv", skip=6,
sep=",", nrows=6000)
spectrum(data11$V2,method="ar")
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_12.csv", skip=6,
sep=",", nrows=6000)
bispec(data11$V2)
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_12.csv", skip=6,
sep=",", nrows=6000)
autcor(data11$V2)
・・・・・・・・
・・・・・・・・
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_24.csv", skip=6,
sep=",", nrows=6000)
plot(data11$V2)
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_24.csv", skip=6,
sep=",", nrows=6000)
spectrum(data11$V2,method="ar")
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_24.csv", skip=6,
sep=",", nrows=6000)
bispec(data11$V2)
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_24.csv", skip=6,
sep=",", nrows=6000)
autcor(data11$V2)
Page13
3)以下のようにテキストデータをコピーしてRの画面にペーストすると
自己相関の変化をグラフで確認できます
下記をコピー&ペースト
par(mfrow=c(4,4))
data11 <- read.table("C:/2024/20240301-0002/20240301-0002_01.csv", skip=6, sep=",", nrows=15000)
autcor(data11$V2)
data11 <- read.table("C:/2024/20240301-0002/20240301-0002_02.csv", skip=6, sep=",", nrows=15000)
autcor(data11$V2)
data11 <- read.table("C:/2024/20240301-0002/20240301-0002_03.csv", skip=6, sep=",", nrows=15000)
autcor(data11$V2)
data11 <- read.table("C:/2024/20240301-0002/20240301-0002_04.csv", skip=6, sep=",", nrows=15000)
autcor(data11$V2)
・・・
data11 <- read.table("C:/2024/20240301-0002/20240301-0002_30.csv", skip=6, sep=",", nrows=15000)
autcor(data11$V2)
data11 <- read.table("C:/2024/20240301-0002/20240301-0002_31.csv", skip=6, sep=",", nrows=15000)
autcor(data11$V2)
data11 <- read.table("C:/2024/20240301-0002/20240301-0002_32.csv", skip=6, sep=",", nrows=15000)
autcor(data11$V2)
Page14
4)以下のようにテキストデータをコピーしてRの画面にペーストすると
バイスペクトルの変化をグラフで確認できます
下記をコピー&ペースト
par(mfrow=c(4,4))
data11 <- read.table("C:/2024/20240301-0002/20240301-0002_01.csv", skip=6, sep=",", nrows=6000)
bispec(data11$V2)
data11 <- read.table("C:/2024/20240301-0002/20240301-0002_02.csv", skip=6, sep=",", nrows=6000)
bispec(data11$V2)
data11 <- read.table("C:/2024/20240301-0002/20240301-0002_03.csv", skip=6, sep=",", nrows=6000)
bispec(data11$V2)
data11 <- read.table("C:/2024/20240301-0002/20240301-0002_04.csv", skip=6, sep=",", nrows=6000)
bispec(data11$V2)
・・・
data11 <- read.table("C:/2024/20240301-0002/20240301-0002_29.csv", skip=6, sep=",", nrows=6000)
bispec(data11$V2)
data11 <- read.table("C:/2024/20240301-0002/20240301-0002_30.csv", skip=6, sep=",", nrows=6000)
bispec(data11$V2)
data11 <- read.table("C:/2024/20240301-0002/20240301-0002_31.csv", skip=6, sep=",", nrows=6000)
bispec(data11$V2)
data11 <- read.table("C:/2024/20240301-0002/20240301-0002_32.csv", skip=6, sep=",", nrows=6000)
bispec(data11$V2)
Page15
実施例:バイスペクトルの変化を確認する
dev.off()
par(mfrow=c(3,2))
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_13.csv", skip=6,
sep=",", nrows=6000)
bispec(data11$V2)
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_14.csv", skip=6,
sep=",", nrows=6000)
bispec(data11$V2)
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_15.csv", skip=6,
sep=",", nrows=6000)
bispec(data11$V2)
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_16.csv", skip=6,
sep=",", nrows=6000)
bispec(data11$V2)
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_17.csv", skip=6,
sep=",", nrows=6000)
bispec(data11$V2)
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_18.csv", skip=6,
sep=",", nrows=6000)
bispec(data11$V2)
Page16
実施例:自己相関の変化を確認する
dev.off()
par(mfrow=c(3,2))
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_13.csv", skip=6,
sep=",", nrows=6000)
autcor(data11$V2)
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_14.csv", skip=6,
sep=",", nrows=6000)
autcor(data11$V2)
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_15.csv", skip=6,
sep=",", nrows=6000)
autcor(data11$V2)
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_15.csv", skip=6,
sep=",", nrows=6000)
autcor(data11$V2)
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_17.csv", skip=6,
sep=",", nrows=6000)
autcor(data11$V2)
data11 <- read.table("C:/20191220/20191220-0022/20191220-0022_18.csv", skip=6,
sep=",", nrows=6000)
autcor(data11$V2)
Page17
解析の詳細・解析結果の解釈・・・については
以下の参考書籍・・・の専門書を読んでください
参考書籍
1:統計数理
1)叩いて超音波で見る―非線形効果を利用した計測
佐藤 拓宋 (著) 出版社: コロナ社 (1995/06)
2)電気系の確率と統計
佐藤 拓宋 (著) 出版社: 森北出版 (1971/01)
3)不規則信号論と動特性推定
宮川 洋 (著), 佐藤拓宋 (著), 茅 陽一 (著)
出版社: コロナ社 (1969)
4)赤池情報量規準 AIC―モデリング・予測・知識発見
赤池 弘次 (著), 室田 一雄 (編さん), 土谷 隆 (編さん)
出版社: 共立出版 (2007/07)
5)ダイナミックシステムの統計的解析と制御
赤池 弘次 (著), 中川 東一郎 (著)
出版社: サイエンス社(1972)
2:超音波技術
1)超音波工学と応用技術
ベ.ア.アグラナート (他共著),青山 忠明 (訳),遠藤 敬一 (訳)
発行年月:1991 出版社: 日ソ通信社
2)超音波入門 (科学普及新書)
エリ・デ・ローゼンベルク 著, 上田光隆 訳
発行年月:1967 出版社:東京図書
参考資料
超音波の相互作用を評価する技術2
http://ultrasonic-labo.com/?p=12202
超音波加工・溶接技術(特開 2021-171909)
http://ultrasonic-labo.com/?p=3963
AIC(情報量規準)を利用した超音波技術
http://ultrasonic-labo.com/?p=1074
超音波技術:多変量自己回帰モデルによるフィードバック解析
http://ultrasonic-labo.com/?p=15785
Page18
<<超音波の音圧データ解析・評価>>
1)時系列データに関して、
多変量自己回帰モデルによるフィードバック解析により
測定データの統計的な性質(超音波の安定性・変化)について解析評価します
2)超音波発振による、発振部が発振による影響を
インパルス応答特性・自己相関の解析により
対象物の表面状態・・に関して、超音波振動現象の応答特性として解析評価します
3)発振と対象物(洗浄物、洗浄液、水槽・・)の相互作用を
パワー寄与率の解析により評価します
4)超音波の利用(洗浄・加工・攪拌・・)に関して
超音波効果の主要因である対象物(表面弾性波の伝搬)
あるいは対象液に伝搬する超音波の非線形(バイスペクトル解析結果)現象により
超音波のダイナミック特性を解析評価します
この解析方法は、
複雑な超音波振動のダイナミック特性を
時系列データの解析手法により、
超音波の測定データに適応させるこれまでの経験と実績に基づいて実現しています。
超音波の伝搬特性
1)振動モードの検出(自己相関の変化)
2)非線形現象の検出(バイスペクトルの変化)
3)応答特性の検出(インパルス応答の解析)
4)相互作用の検出(パワー寄与率の解析)
注:「R」フリーな統計処理言語かつ環境
autcor:自己相関の解析関数 bispec:バイスペクトルの解析関数
mulmar:インパルス応答の解析関数 mulnos:パワー寄与率の解析関数
Page19
解析ソフトについて
TIMSAC for R package 統計数理研究所 November 1, 2006
TIMSAC(TIMe Series Analysis and Control program package) は,統計数理研
究所で開発された時系列データの解析,予測,制御のための総合的プログラムパッ
ケージです.・・・
TIMSAC はFORTRANで書かれたプログラムですが,ユーザーが作成した
FORTRAN,C,Java のプログラムにこのライブラリをリンクすることにより,よ
り扱い易い環境が実現されました.
バイスペクトルの解析関数
bispec() : バイスペクトルの計算
自己相関の解析関数
autcor() : 直接法による自己共分散関数の計算
3)TIMSAC for R package
http://jasp.ism.ac.jp/ism/timsac/
Page20
参考データ
解析結果
自己相関(最大 200Lag)
音圧データ1:青 音圧データ1:赤 音圧データ2:青 音圧データ2:赤
バイスペクトル(最大周波数 62MHz)
音圧データ1:青 音圧データ1:赤 音圧データ2:青 音圧データ2:赤
100μ秒でこのような音圧変化を実現することが、新しい超音波制御技術です