1/13ページ
ダウンロード(3.6Mb)
超音波の非線形解析データから、新しい超音波利用を導く
超音波システム研究所は、
多変量自己回帰モデルによるフィードバック解析技術を応用した、
「超音波の伝搬状態を測定・解析・評価する技術」を利用して
超音波利用に関するコンサルティング対応を行っています。
超音波テスターを利用したこれまでの
計測・解析・結果(注)を時系列に整理することで
目的に適した超音波の状態を示す
新しい評価基準(非線形現象の解析パラメータ)を開発しました。
注:
非線形特性(高調波の発生特性)
応答特性
ゆらぎの特性
相互作用による影響
統計数理の考え方を参考に
対象物の音響特性・表面弾性波を考慮した
オリジナル測定・解析手法を開発することで
振動現象に関する、詳細な各種効果の関係性について
新しい理解を深めています。
その結果、
超音波の伝搬状態と対象物の表面について
新しい非線形パラメータが大変有効である事例による
実績が増えています。
特に、洗浄・加工・表面処理効果に関する評価事例・・
良好な確認に基づいた、制御・改善・・・が実現します。
このカタログについて
| ドキュメント名 | 超音波の伝搬状態・非線形現象を評価する技術-Ver3 |
|---|---|
| ドキュメント種別 | 製品カタログ |
| ファイルサイズ | 3.6Mb |
| 登録カテゴリ | |
| 取り扱い企業 | 超音波システム研究所 (この企業の取り扱いカタログ一覧) |
この企業の関連カタログ

このカタログの内容
Page1
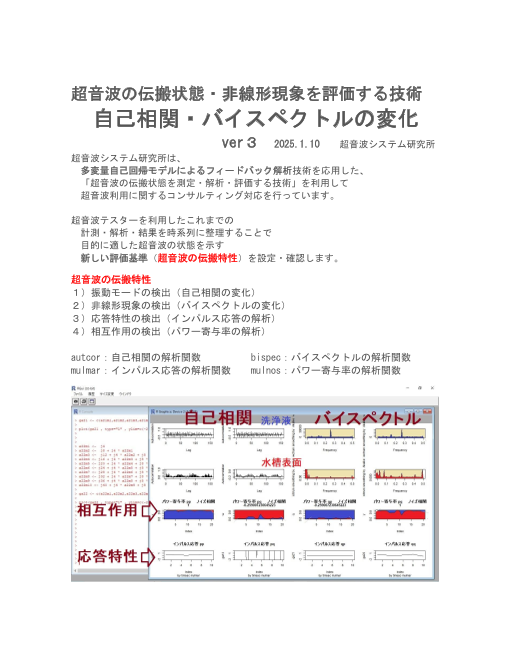
超音波の伝搬状態・非線形現象を評価する技術
自己相関・バイスペクトルの変化
ver3 2025.1.10 超音波システム研究所
超音波システム研究所は、
多変量自己回帰モデルによるフィードバック解析技術を応用した、
「超音波の伝搬状態を測定・解析・評価する技術」を利用して
超音波利用に関するコンサルティング対応を行っています。
超音波テスターを利用したこれまでの
計測・解析・結果を時系列に整理することで
目的に適した超音波の状態を示す
新しい評価基準(超音波の伝搬特性)を設定・確認します。
超音波の伝搬特性
1)振動モードの検出(自己相関の変化)
2)非線形現象の検出(バイスペクトルの変化)
3)応答特性の検出(インパルス応答の解析)
4)相互作用の検出(パワー寄与率の解析)
autcor:自己相関の解析関数 bispec:バイスペクトルの解析関数
mulmar:インパルス応答の解析関数 mulnos:パワー寄与率の解析関数
Page2
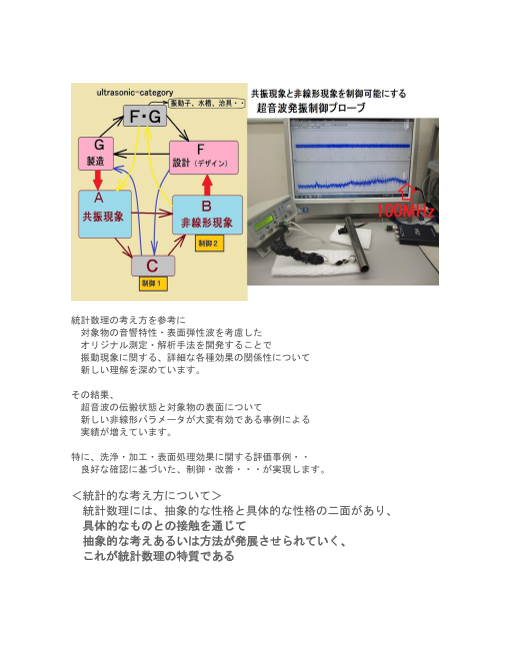
統計数理の考え方を参考に
対象物の音響特性・表面弾性波を考慮した
オリジナル測定・解析手法を開発することで
振動現象に関する、詳細な各種効果の関係性について
新しい理解を深めています。
その結果、
超音波の伝搬状態と対象物の表面について
新しい非線形パラメータが大変有効である事例による
実績が増えています。
特に、洗浄・加工・表面処理効果に関する評価事例・・
良好な確認に基づいた、制御・改善・・・が実現します。
<統計的な考え方について>
統計数理には、抽象的な性格と具体的な性格の二面があり、
具体的なものとの接触を通じて
抽象的な考えあるいは方法が発展させられていく、
これが統計数理の特質である
Page3
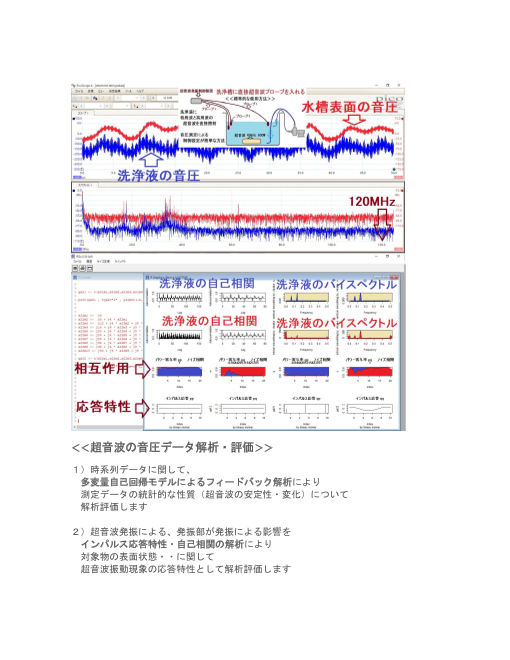
<<超音波の音圧データ解析・評価>>
1)時系列データに関して、
多変量自己回帰モデルによるフィードバック解析により
測定データの統計的な性質(超音波の安定性・変化)について
解析評価します
2)超音波発振による、発振部が発振による影響を
インパルス応答特性・自己相関の解析により
対象物の表面状態・・に関して
超音波振動現象の応答特性として解析評価します
Page4
3)発振と対象物(洗浄物、洗浄液、水槽・・)の相互作用を
パワー寄与率の解析により評価します
4)超音波の利用(洗浄・加工・攪拌・・)に関して
超音波効果の主要因である対象物(表面弾性波の伝搬)
あるいは対象液に伝搬する超音波の
非線形(バイスペクトル解析結果)現象により
超音波のダイナミック特性を解析評価します
Page5
この解析方法は、
複雑な超音波振動のダイナミック特性を
時系列データの解析手法により、
超音波の測定データに適応させる
これまでの経験と実績に基づいて実現しています。
注:解析には下記ツールを利用します
注:OML(Open Market License)
https://www.ism.ac.jp/ismlib/jpn/ismlib/license.html
注:TIMSAC(TIMe Series Analysis and Control program)
https://jasp.ism.ac.jp/ism/timsac/
注:「R」フリーな統計処理言語かつ環境
https://cran.ism.ac.jp/
バイスペクトルは、以下のように
周波数 f1、f 2、f1 + f 2 のスペクトルの積で表すことができる。
B( f1 , f 2 ) = X( f1 )Y( f 2 )Z( f1 + f 2 )
主要周波数が f1 であるとき、
f1 + f1 = f 2、f1 + f 2 = f3 で表される
f 2、f3という周波数成分が存在すれば、バイスペクトルは値をもつ。
これは主要周波数 f1 の
整数倍の周波数成分を持つことと同等であるので、
バイスペクトルを評価することにより、高調波の存在を評価できる。
Page6
<<超音波システム>>
超音波の音圧測定・解析システムと超音波発振制御システム
http://ultrasonic-labo.com/?p=1546
超音波発振システム(1MHz、20MHz)
http://ultrasonic-labo.com/?p=18817
超音波システム(音圧測定解析、発振制御)
http://ultrasonic-labo.com/?p=19422
Page7
超音波の音圧測定解析システム「超音波テスターNA」
http://ultrasonic-labo.com/?p=16120
統計的な考え方を利用した超音波
http://ultrasonic-labo.com/?p=12202
超音波技術:多変量自己回帰モデルによるフィードバック解析
http://ultrasonic-labo.com/?p=15785
Page8
超音波計測装置(超音波テスター)を利用した測定事例
http://ultrasonic-labo.com/?p=1685
超音波発振・計測・解析システム(超音波テスター)
http://ultrasonic-labo.com/?p=7662
超音波の音圧測定解析データを公開
http://ultrasonic-labo.com/?p=2387
Page9
超音波<測定・解析>システム
http://ultrasonic-labo.com/?p=1000
超音波プローブの発振制御による振動評価技術
http://ultrasonic-labo.com/?p=15285
超音波システム(音圧測定解析、発振制御 10MHz タイプ)
http://ultrasonic-labo.com/wp-
content/uploads/a11b84107286cec4d7eb0b5e498d2636.pdf
詳細に興味のある方は
超音波システム研究所にメールでお問い合わせください。
メールアドレス info@ultrasonic-labo.com
Page13
以上