1/8ページ
ダウンロード(2.2Mb)
<< 超音波の音圧データ解析 >>
<< 超音波の音圧データ解析 >>
1)時系列データに関して、
多変量自己回帰モデルによるフィードバック解析により
測定データの統計的な性質(超音波の安定性・変化)について
解析評価します
2)超音波発振による、発振部が発振による影響を
インパルス応答特性・自己相関の解析により
対象物の表面状態・・に関して
超音波振動現象の応答特性として解析評価します
3)発振と対象物(洗浄物、洗浄液、水槽・・)の相互作用を
パワー寄与率の解析により評価します
4)超音波の利用(洗浄・加工・攪拌・・)に関して
超音波効果の主要因である対象物(表面弾性波の伝搬)
あるいは対象液に伝搬する超音波の
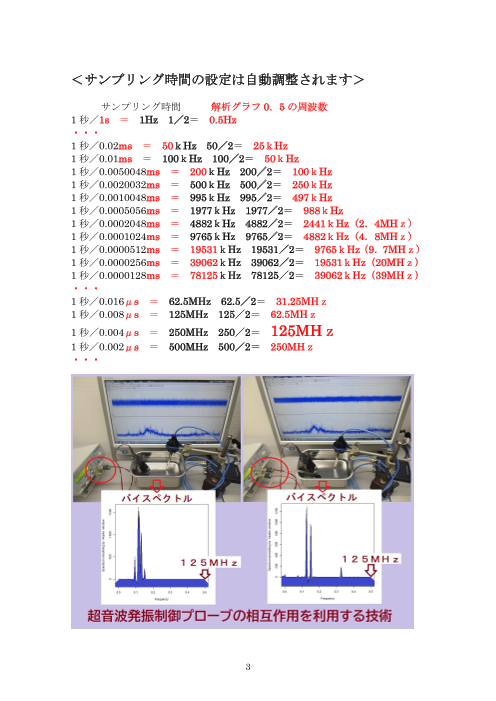
非線形(バイスペクトル解析結果)現象により
超音波のダイナミック特性を解析評価します
この解析方法は、
複雑な超音波振動のダイナミック特性を
時系列データの解析手法により、
超音波の測定データに適応させる
これまでの経験と実績に基づいて実現しています。
注:解析には下記ツールを利用します
注:OML(Open Market License)
https://www.ism.ac.jp/ismlib/jpn/ismlib/license.html
注:TIMSAC(TIMe Series Analysis and Control program)
https://jasp.ism.ac.jp/ism/timsac/
注:「R」フリーな統計処理言語かつ環境
https://cran.ism.ac.jp/
このカタログについて
| ドキュメント名 | 音圧解析の初歩ver3 |
|---|---|
| ドキュメント種別 | 製品カタログ |
| ファイルサイズ | 2.2Mb |
| 登録カテゴリ | |
| 取り扱い企業 | 超音波システム研究所 (この企業の取り扱いカタログ一覧) |
この企業の関連カタログ

このカタログの内容
Page1
音圧解析の初歩 Ver3
超音波テスター(音圧測定システム)
超音波システム研究所
1
Page2
サンプリング時間の表示方法
入力
data11 <- read.table("C:/2011/201101.csv", skip=0, sep="," , nrows=10 )
data11
応答(パソコンの画面表示)
V1 V2 V3
1 Time Channel A Channel B
2 (ms) (V) (V)
3 0.00000000 0.33310950 -0.07290872
4 0.00256000 0.07199316 0.03616443 グラフ 0.5=195kHz
5 0.00512000 -0.16211430 -0.00927763
6 0.00768000 0.06299020 -0.09109775
7 0.01024000 0.05398724 0.13611260
8 0.01280000 -0.16211430 0.15430160
9 0.01536000 0.10800500 -0.22745450
10 0.01792000 0.27008880 -0.23654900
>
1 秒/0.00256000ms = 390.625kHz 390/2= 195kHz
data11 <- read.table("C:/2011/2011103.csv", skip=0, sep="," , nrows=10 )
data11
V1 V2 V3
1 Time Channel A Channel B
2 (ms) (V) (V)
3 0.00000000 -0.03604236 -0.11838130
4 0.00064000 -0.04504532 -0.06381420 グラフ 0.5=781kHz
5 0.00128000 -0.05404828 -0.02746666
6 0.00192000 -0.07205420 0.02706992
7 0.00256000 -0.05404828 0.09067049
8 0.00320000 -0.03604236 0.10885950
9 0.00384000 -0.01803644 0.09976501
10 0.00448000 -0.03604236 0.07248146
1 秒/0.00064000ms = 1562.5kHz 1562/2= 781kHz
注:解析には下記ツールを利用します
注:OML(Open Market License)
https://www.ism.ac.jp/ismlib/jpn/ismlib/license.html
注:TIMSAC(TIMe Series Analysis and Control program)
https://jasp.ism.ac.jp/ism/timsac/
注:「R」フリーな統計処理言語かつ環境
https://cran.ism.ac.jp/
2
Page3
<サンプリング時間の設定は自動調整されます>
サンプリング時間 解析グラフ 0.5 の周波数
1 秒/1s = 1Hz 1/2= 0.5Hz
・・・
1 秒/0.02ms = 50kHz 50/2= 25kHz
1 秒/0.01ms = 100kHz 100/2= 50kHz
1 秒/0.0050048ms = 200kHz 200/2= 100kHz
1 秒/0.0020032ms = 500kHz 500/2= 250kHz
1 秒/0.0010048ms = 995kHz 995/2= 497kHz
1 秒/0.0005056ms = 1977kHz 1977/2= 988kHz
1 秒/0.0002048ms = 4882kHz 4882/2= 2441kHz(2.4MHz)
1 秒/0.0001024ms = 9765kHz 9765/2= 4882kHz(4.8MHz)
1 秒/0.0000512ms = 19531kHz 19531/2= 9765kHz(9.7MHz)
1 秒/0.0000256ms = 39062kHz 39062/2= 19531kHz(20MHz)
1 秒/0.0000128ms = 78125kHz 78125/2= 39062kHz(39MHz)
・・・
1 秒/0.016μs = 62.5MHz 62.5/2= 31.25MHz
1 秒/0.008μs = 125MHz 125/2= 62.5MHz
1 秒/0.004μs = 250MHz 250/2= 125MHz
1 秒/0.002μs = 500MHz 500/2= 250MHz
・・・
3
Page4
音圧レベルの表示
入力
data11 <- read.table("C:/20111/2011102.csv", skip=6, sep=",")
mean(data11$V2)
mean(data11$V3)
var(data11$V2)
var(data11$V3)
range(data11$V2)
range(data11$V3)
応答(パソコンの画面表示)
> data11 <- read.table("C:/20111022w/20111022-0412.csv", skip=6, sep=",")
> mean(data11$V2) CH1 の平均値
[1] -0.001047526
> mean(data11$V3) CH2 の平均値
[1] 3.430622e-05
> var(data11$V2) CH1 の分散値
[1] 0.009286384
> var(data11$V3) CH2の分散値
[1] 0.001448241
> range(data11$V2) CH1 の最小・最大値
[1] -0.4412366 0.4141362
> range(data11$V3) CH2の最小・最大値
[1] -0.1547288 0.1361126
>
注意
統計処理を行うために、測定値が自動的に、規格化(正規化)されています
バイスペクトルについて理解が深まるまでは
最大・最小値、分散値、平均値 を利用することを推奨します
絶対値としての音圧は、測定データのグラフから読み取ってください
その値に対する平均や分散を上記の処理で推定して利用します
4
Page5
具体例
data11 <- read.table("C:/20191220/191220-0018/20191220-0018_15.csv", skip=6,
sep=",")
mean(data11$V2)
mean(data11$V3)
var(data11$V2)
var(data11$V3)
range(data11$V2)
range(data11$V3)
グラフ青 音圧レベル 360mV
グラフ赤 音圧レベル 16mV
5
Page6
音圧・周波数の変化を目視確認する
6
Page7
音圧・周波数の変化を音圧データの解析で確認する
7
Page8
様々な条件で、繰り返し確認すると、
音圧データのグラフを見ることで解析結果は推測できます
以上
8